
(under evolution)
Abstract
Entities such as the Web, mankind, life, the earth, the solar system,
the Milky way, and our universe are viewed as massive
dissipative/replicative structures. This paper will examine the
structure and process of massive dissipative/replicative structures.
In addition, it will examine the concept of massive dissipative/replicative
structures and what are the necessary issues in structuring the scientific
understanding of the phenomena. The methodology of comparative science and relational complexity
is suggested to help in the construction and analysis of scientific theories.
This paper will examine the structure and process of massive dissipative/replicative structures. In addition, it will examine the concept of massive dissipative/replicative structures and what are the necessary issues in structuring the scientific understanding of the phenomena. Lastly, I will suggest a methodology that can help in the construction and analysis of scientific theories.
Dis -sipa -tive: dis- = apart,
supare = to throw (to throw apart)
Re -plica -tive: re = again, plicate = to fold
(to refold)
Structure: structura = a fitting together
In particle physics, the word "dissipative" is not use extensively, for they assert that quantum structures are not dissipative. On the other hand, physics tells us there is some equivalence between mass and energy, and quantum structures can exchange energy and often "spontaneously emit" energy in the form of bosons. This use of the word "spontaneous" is analogous to the unjustified finesse in using the phrase "spontaneous generation" taken by pre-Pasteur scientists regarding life. The slight of hand in particle physicist's phrase "spontaneously emit or decay" alerts one to the fact that physical theories cannot explain the underlying process, except by a non-ontological satisfying mathematical operation (quantum mechanics) that mimics the behavior. Because of this, I will generalize the notion of "dissipation" to include the notion of "thermodynamic." That is, "thermodynamic" means to include "dissipative" of energy or matter - space and time. Since all physical systems are "thermodynamic," then all systems are "dissipative," including bosons and the universe.

Ilya Prigogine [ Prigogine84, 97] has put forward that dissipative structures do not obey Boltzmann's order principle, because a dissipative structure is not in equilibrium. Moreover, one must admit that the universe is not in equilibrium, it is forever changing: "evolving" as it were. This observation is key to understanding how the "evolution" of the our universe and its embedded structures will proceed. The century old hypothesis of "heat death" of the universe, based on the second law of thermodynamics is no longer the most reasonable scenario because it appears that the universe is a non-equilibrium structure [Smolin97]. It is not clear, what the universe is "dissipating" but in some sense you can imagine it "dissipating" space/time.
On the other hand, before the evolution of the universe and its embedded structures can be understood, a new method of characterization of the notion of 'system' must be formulated. For one major flaw in the scientific enterprise has been the lack of a methodology for conceptual integration and analysis between "a system" and its context. Viewing the universe as a "closed" or "isolated" system is no longer acceptable.
When examining massive dissipative structures, such as galaxy systems, it is fairly clear now that a significant property of them has been primarily and largely ignored by the scientific community. Massive dissipative structures should be called massive dissipative/replicative structures, for the property of replication of microstructures has been largely de-emphasized in "non living" massive dissipative structures. The classic example is the creation of more atomic nuclei in stars (which is a form of replication). Moreover, certain quanta are considered "elementary particles" and in cosmology are posited, de novo, in the beginning of the big bang. De novo positing of billions of any kind of "string" or "particle," such as leptons, begs the question of their origin. That replication of these structures occurred seems to be a more reasonable hypothesis, even though we may never know exactly how (i.e., the internal mechanism of) replication of the particle or string occurred. It is not clear, what the universe is "replicating" but in some sense you can imagine it "replicating" time/space.
In addition, the property of dissipation has been largely de-emphasized in "living" massive replicative structures (such as Gaia [Lovelock87], Hypersea[ McMenanim94], and Metaman[Stock93]). But the relations between dissipation and replication are crucial in understanding how the world works. One of the problems has been that both processes, dissipation and replication, must go hand in hand when modeling natural systems, but explicit coupling has not been considered before. It is posited that in reality (e.g., our universe), replication and dissipation cannot be separated: one implies the other.
When discussing the creation, evolution, and the underlying nature
of long-term natural entities, there has been a gradual realization that
using reductionistic methods and terminology has lead to an impasse in
understanding. For example, the current crisis in quantum mechanics
(the disconnect with relativity) has lead several researchers [Bohm93,
Smolin97,
Prigogine97,
Rosen91]
to question the underlying characterization. Particle physics has
had to turn to cosmology and astrophysics to help in finding models of
the creation and evolution of the microscopic entities based on
the state of the entire universe. Also recently, the
incompleteness of the neo-darwinian model of evolution has been exposed
by questions posed by researchers, such as, Margulis and Lovelock on the
relationship between the biosphere, the solar system, and life.
The origin of life also seems shrouded in mystery, given that it is highly
possible that the origin of life occurred within the depths of the earth's
crust [Gold98],
where biologists have little clue of the metabolic and genetic processes
of these organisms. Finally, can the future of mankind be addressed
without understanding the role of the Gaia [
Lovelock87] and Hypersea [McMenanim94] hypotheses and their connection to the future evolution
of the Internet and our future mind children?
On the other hand, scientific progress has been practically synonymous
with the methodology of reductionism and the atomic hypothesis. If science
is practically defined by the notions of "simplifying the problem" and
analysis of the working of the parts of a system, then what techniques
and methodologies are alternatives or additions to this most successful
approach.
There are very few scientists that would admit to being reductionists,
but we all are, to a large degree, inheritors of Newton's
brilliant mistake [Rosen91]. But, besides lamenting the sins
of reductionism [Rosen 91] [Goodwin
96] [Oyama86]
and pointing out its weaknesses, there needs to be a methodology for going
beyond the criticism and helping to generate new ways of understanding
and building conceptual models which include the both the characterization
of context and the "system" of complex phenomena.
Rosen has pointed out the main problem with most scientific work lies in the characterization of the environment of the studied system. Or rather, he points out, the problem is the lack of characterization of the environment or "surrounding" context of the "system," by the "hidden" assumptions in the scientific models. Robert Rosen suggested that current science is missing a major mode of entailment [Rosen91]. Although his argument is convincing for most who are familiar with it (very few know about it), his prescription has been largely ignored. Besides the fact that he suggests unconventional mathematics, category theory, relative to his audience, biologists, one possible reason for the lack of notice is that Rosen does not give a concrete methodology for constructing a theory of "the system" within its context. Although, his approach and technique cannot be faulted, other than for its abstractness and dearth of concrete examples.
Rosen rigorously shows the limits of current analytic science (implicitly including quantum gravity and string theory) symbolized by Newtonian physics and Turing computation. He argues that science are not using all available modes of entailment in its fight against complexity. Current science avoids the why questions, for answering the why question could involve teleology. Reductionistic science unnecessarily avoids asserting final cause because it does not want to be accused of asserting unjustified tautologies (circular reasoning - "finite" or "infinite"). However, in creating theory (a model of reality) which may correspond to reality, one must assert final cause to entail anything of significance. For example, normal boolean logic implies a final cause based on the definition of implies, (p implies (p v ~p)): which is Aristotle's excluded middle, a basis of "discrete logic". Some mathematical systems, such as intuitionistic logic, do not assume the excluded middle. Rosen calls this fabrication of theory, a necessary part of science and mathematics. He asserts that fabrication of the modeling relation (his terminology for his particular representation of "theory") is an art. I assert one can do better by using a methodology, comparative complexity, that systematizes the fabrication and analysis of theory by the precise use of analogy.
In technical terms, comparative complexity is attaching semantics in a disciplined way to essentially syntactic models (homomorphisms -- fabricated tautologies) to interrelate those homomorphisms in a coherent and semantically meaningful way (in the form of a syntactic-semantic model), based on careful observation and analysis of natural systems. Category theory, or topos theory specifically, are examples of a kind of mathematics that can use abstract forms of entailment that can entail final cause, but divorced from semantics they are just another kind of formalism. Formalism are just that, games to be played with no meaning and hence no use. The use comes in marrying syntax and semantics in useful way, so entailment and analogy can be used in a rigorous and meaningful way.
The use of analogy implies crossing between contexts. Unfortunately, the ignoring of context deemed irrelevant, is a mark of the facile scientist. Specialization in specific scientific domains is the characterization of most of science today. Clearly the scientific justification of the biologist to "ignore" phenomena such as quarks and neutrinos and the possible "heat death" of the universe seems justified, because it seems that these types of phenomena have no relevance to biology, i.e., the life systems. However, the notion of dissipative structures, once thought as only strictly relevant to the domain of non-equilibrium chemical thermodynamics, has been shown to be highly relevant to "life" because life is based on non-equilibrium chemical thermodynamics. Suddenly, the evolution of neutrinos, probably related to the evolution the non-equilibrium thermodynamics of the universe, no longer seems as remote to biology as it had before.
The non acceptance, misbelief, or ignorance of Rosen's criticism of limitations of computer science and current physics is also understandable for although quantum mechanics is not ontological satisfying and only accounts for the micro-world of particle physics, it still has the most precise predictive power of all of science. But physicists, are analogous to the biologist, for not seeing the relevance of "life" in helping understand the evolution of the universe and in ignoring phenomena that may give analogous clues to the underlying processes of the big bang, which are hidden by the Planck wall. For example, the question of the "function" of the tau, muon, and electron neutrinos in the big-bang is not answerable in current cosmological theories, for they adhere to the strict Newtonian paradigm dictum: not to ask why questions. But, analogy across seemly disparate but vaguely similar phenomena can give us hints to some of the answers to precise abstract questions not asked by physics.
With the realization that the world is primarily made of dissipative structures, and not equilibrium or linear structures as modeled in physics, the mistake of poor characterization of the surrounding context and its effect on the "system" is even more troubling. For the evolution of a dissipative structure is significantly determined by its surrounding context. Moreover, to the realization that the world is primarily made of replicative structures, even in the non-living part, argues that both Newtonian biology (neo-Darwinism) and Newtonian physics (quantum field theory and relativity) are missing something. On the other hand, we cannot turn to holism or vitalism for they have no useful methods that make scientific sense and do not provide intellectual traction for understanding.
Comparative complexity is the analysis and comparison of analogous fabricated models of natural systems to extract the underlying process-structure of existence. That is, it is important to extract both structure (the how) and function (the why) of the underlying models of natural systems. In its primitive and vaguest form, comparative complexity involves the use of scientific analogs and metaphors between domains of science: this has been going on since the dawn of science. Unfortunately, analogy and metaphor is viewed, with justified skepticism, as "unscientific." But, using the clues suggested by Rosen, there is now a good chance that more precise methods of analogy and metaphor akin to the mathematical category theory can be developed and used to good effect. The idea is to "throw away" the details in terms of "state" and find the correct abstract functions and structures of natural systems depending on the desired level of abstraction and relation to other natural systems, hence their models.
For example, Topos theory, and the brilliant work of Grothendieck and the Bourbaki Group has dominated much of mathematics the previous half century, but the argot of abstract mathematics has formed a high and obscure wall that are difficult to climb or see clearly into. No doubt concepts pointed to with such words as "sheaths," "etales," "skew fields", yada yada, are key to analyzing the world, but they are hard to relate to the real world.
Historically, significant progress has been accomplished by using analogous methods, concepts, and processes of one domain to help in another. For example, Boltzmann viewed himself as the Darwin of physics and proceeded to do evolutionary analysis based on combinatorics of atoms that advanced the field of thermodynamics. Chemists like Dalton viewed themselves as Newtonians in the realm of material substances. W.R. Hamilton made the mechanical analogy from Maxwell's equations for optics. It is also true, there have been many (in fact, probably most attempts) that have less than successful. It is the nature of things that it takes a great deal of time and scientific effort to learn and progress from the incorrect or imprecise analogies, as did previous examples. In addition, bad, imprecise, or poor analogies can have, and have had, negative or terrible political or social mpact (Social Darwinism -> Nazism, Political Hegelism -> communism, and Chemical Psychology (Psychiatry)-> the use of cocaine-like drugs like Ritalin on school children).
Nevertheless, other notoriously vague and initially incorrect models and ideas, such as Lamarck's acquired characteristics and Hegel's dialectic still have some traction in examining the faults of reductionism and still posing important questions. Stephen Jay Gould's analysis in his book, The Structure of Evolutionary Theory, is a excellent example of one way of utilizing both the conceptual misapplication and conceptual correctness of scientific work whatever the source. Although, it is clear significant progress has to be made, still. For example, Gould, despite his wide range of knowledge in biology and his seeming encyclopedic treatment of evolution, one cannot help but be puzzled with the fact he knew Lynn Margulis, but nevertheless, makes no reference to her work in symbiosis -- a vital piece of evolutionary theory. His omission is curious, for it may indicate the inherent difficulty in most scientists correctly recognizing the appropriate metaphors and analogies slightly outside their limited area of expertise.
On the other hand, science, as well as most things connected to the Web, is now proceeding in a much more rapid pace. With the development of the science of complexity, all physical phenomena have some analytic techniques that can be applied. Although just in its beginnings, complexity science with the notions of chaos, order, and the edge-of-chaos/edge-of-order are being linked to complex phenomena, such as the living cell, life, and mankind. No longer can scientists and academics dismiss non-linear phenomena as being too difficult. But, there is the danger of just using the poor tools of "physics" to the problem. And there is the risk of the normal obscuring of misplaced or weak analogies, such as attributing oxymoronic generalizations such as "self-organization" or "self-criticality" everywhere. And clearly excessive abstraction without a systemic approach -- leads to religious-like science or incomprehensible mathematics that only high priests can intimidate the un-credentialed or the un-blessed.
The biggest problem with studying phenomena is the complexity. Again, even in "simple" entities (they have very little "state" or invariant properties) such as studying "neutrinos," one is forced to consider the evolution of the universe. Reductionistic techniques of the sciences (that is: practically all precise techniques of science) are confronted with "structures" that are processes within processes, within processes, within processes, ad nauseam. Non in-situ analysis is endangered by inadvertent modification or ignoring the effects of one of the underlying processes. For example, the current methodology of renormalization, is just an approximation scheme for particle physics' theories. More recently, the current method of trying to "find" chaotic and ordered processes in natural systems is proceeding with great enthusiasm. But, if entities or "systems" contain both chaotic processes and order processes, which in turn, contain both chaotic and ordered processes, ad nauseam, then how can the analysis proceed?
Supposedly "less reductionistic" techniques of the life sciences, typified by Stephen Jay Gould's historical approach, are not the complete answer either. Gould's artificial separation of the "historical" life sciences with the "repeatable" and experimental sciences, such as physics and chemistry is not useful distinction. Although eloquent and rigorous in most of his reasoning, Gould's supposition that biology is mostly "historical" (in his words: contingent) in nature (hence he can dismiss the applicably of physics) is not founded in a scientific basis. Gould, in restricting his analysis to "life", assumes that "non-life" phenomena or laws have no relevance. Random historical events are thought to rule the domain of life. However, the universe, if we believe the physicist has the same contingency structure (global randomness) as biology. Rosen has pointed out [Chapter 11, Life Itself] that strict evolutionists, such as Gould, are also following the reductionistic dictum of not asking why questions, partly to blunt criticism of the hard sciences, for not being "scientific" enough.
Although biology is more "historical" (this is, dependent on properties
of earth's evolution) than physics (dependent on the properties of the
universe's evolution) and some of the "laws" of evolution may have different
"parameters" in some other "life" supporting planet; nevertheless,
there are still "laws" of evolution that are not currently understood,
and the general form of the "laws" are most likely to be applicable for
all life in the universe. But Gould's main point is valid: that biology
is not just complex physics. That is, the concepts, methods,
and techniques of physics cannot be directly applied without very judicious
understanding of the process structure of biology. Rosen's detailed analysis
elucidates the theoretical limits of the current physical theories such
as current cosmological theories and computational approaches, typified
by fractals, artificial life, and chaos theory. He points out physics
can benefit from metaphors of living systems just as well as biology has
used metaphors from physics and chemistry.
It's a mystery what constitutes matter and how it evolved.
All those being interested, are frustrated by the Planck wall. Because
matter seems to be more process than structure, finding patterns below
the Planck wall is going to be difficult. However, the "history"
of the universe and its embedded process structures have vague
similarities. It highly likely that processes below the Planck wall
exhibit analogous forms at higher levels of complexity. By examining this
"history" of the universe precisely, these similarities, such as the evolution
of galaxies to the evolution life and evolution of cyberspace, common patterns
can be noticed.
Moreover, mathematics and information science has analyzed in detail many complex-simple "systems" both in the continuous and discrete manner, such as, 1) Emmy Noether's theorems linking "laws of conservation" and "symmetries" and 2) the finite Sporadic Groups that underlie some of those symmetries.
The task, then, is to be able to represent (encode) and analyze (decode), to as much accuracy as possible, the processes within processes with processes, etc. Armed with a better understanding of phenomena at all levels of complexity and having a methodology of representing nested processes of processes (like Rosen's category theory), then once an underlying a "general" process is understood, it can be used to analyze, any "systems" that have that process embedded.
The general processes, such as chaos and order (in their science of complexity meaning), although very useful in general understanding, cannot be applied without characterizing the specific types of chaos and order. Mathematical models of deterministic chaos assume that the underlying "objects" are infinitely small points. This does not occur in the real world. For example, chaotic particles (particles contained in a chaotic environment, as in the sun) behave differently from chaotic atoms, as in Jupiter: as does chaotic quanta (i.e., quark soup in the big bang). But, there are some common features between chaotic particles and chaotic atoms, which is partially captured by the study of mathematical chaos. The chaos of the atoms in the earth do have some common features of the chaos of the particles in the sun, but there are differences also. Moreover, Prigogine [Prigogine97] and Rosen [Rosen 91] has recently shown that some of the basic assumptions of most particle physics and cosmology are unwarranted both in their models (quantum mechanics) and methods (encoding into Hilbert spaces).
If all "natural structures" in the universe are dissipative/replicative structures 1, then understanding the phenomenology of dissipative/replicative structures is the first order of business, for this is the overall process structure of the all phenomena. The second order of business is understand the phenomena of replicative structures and the relationship between dissipation and replication for each level of material complexity. The task is to characterize, similar to Rosen's methodology, a set of formalizations (informally a metaphor) of a dissipative/replicative structure. The formalizations must include both material and functional characterizations that are related to some degree. This book will not present a formalization or a set of formalizations, but discuss the important concepts necessary in discovering, formulating, and constructing such a set of formalizations and their relations along with a methodology of comparing "words" (such as etales and supersingular primes) and their associated percepts and concepts in a more systemic way. This is opposed to the standard, ad-hoc "art" of creating mathematics and science as it is done today.
And to hear the sun, what a thing to believe,
But it's all around if we could but perceive.
Graeme Edge
For last year's words belong to last year's language and next year's words await another voice.
T.S. Eliot
Words! Words! Words! I’m so sick of words! I get words all day through;
First from him, now from you! Is that all you blighters can do?
Liza Doolittle
Everybody must use words, even the mathematicians. There is a problem with this and the running to equations and quantification does not solve all the problems. There are modeling "traps" that one can get into. Specifically Robert Rosen has said:
As we saw in the preceding section [Rosen's explanation of physics view of organization], the word "organization" has been synonymized with such things as "heterogeneity" and "disequilibrium" and ultimately tied to improbability and nonrandomness. These usages claim to effectively syntacticize the concept of organization but at the cost of stripping it of most of its real content.
Indeed, when we use the term "organization" in natural language, we do not usually mean "heterogeneous," or "nonrandom," or "improbable." Such words are compatible with our normal usage perhaps but only as weak collateral attributes. This is indeed precisely why the physical concept of organization, as I have described above, has been so unhelpful; it amounts to creating an equivocation to replace "organization" by these syntactic collaterals. The interchange of these two usages is not at all a matter of replacing a vague and intuitive notion by an exact, sharply defined syntactic equivalent; it is a mistake.
Lies, Damn Lies, and Statistics
Lies, Damn Lies, and Politics
Lies, Damn Lies, and Physics
Lies, Damn Lies, and Mathematics
Lies, Damn Lies, and Information Science
Lies, Damn Lies, and Religion
Good Science is my religion,
and I have faith in reason.
All marketers
tell lies
tell stories.
-- Seth Godin
Lies, Damn Lies, and the Axiom of Choice
A question is how can we ameliorate the ad-hoc and sloppy choosing of words in science and semi ad-hoc attaching to equations as to try to attach meaning, and then running experiments to rationalize the simplified model. Obviously this has been how some good science has been and is being done, but can we improve it? Plus there is enough "relational science" where simple physical experiments cannot be done in a reasonable way. There is a Tower of Babel in science.
Another question is how can we ameliorate the semi-ad-hoc and sloppy choosing of words in mathematics and demi ad-hoc attaching to equations as to try to attach meaning, and then running of examples to rationalize the abstracted model of words. Obviously this has been how some interesting mathematics has been and is being done, but can we improve it? Plus there is enough "information science" where simple gedanken experiments cannot be done in a simple computational way. There is a Tower of Babel in mathematics.
Latinated and Greekified words such as "entropy" are confusing and obscure, and now there are several kinds of "entropy" -- that is: Tsallis entropy, Shannon entropy, Gibbs entropy, von Neumann entropy. Moreover, there is a overloading of common words in mathematics such as: Banach Space, Baire Space, Luzin Space, Suslin Space, and Radon Space. The balkanization of science and mathematics through the growth in their complexity is in force here. Confusion and ambiguity how these different notions of "entropy" and "space" relate semantically is partly due to the ad-hoc construction of science and mathematics.
The false dichotomy between waves and particles in the quantum world is the most obvious where much ink has been spilled on these simple and necessarily incomplete models; although, it is natural this has happened.
Let us review where these words came from and how they evolved.
Energy--Mass--Space--Time. Quantum foam.
Fire -- Earth -- Air -- Water. Aether.
What's in a name?
That which we call a rose.
By any other name would smell as sweet.
Juliet
Energy: Ancient Greek ἐνέργεια energeia; "activity, operation"
Mass: Late Middle English: from Old French masse, from Latin massa, from Greek maza 'barley cake'; perhaps related to massein 'knead'
Space: Middle English: shortening of Old French espace, from Latin spatium; room
Time: Old English tīma, of Germanic origin; related to tide, which it superseded in temporal senses. The earliest of the current verb senses (dating from late Middle English) is 'do (something) at a particular moment'
IT ALL STARTED WITH THE GREEKS
The Greeks had the simple idea that the world was made of Fire -- Earth -- Air -- Water. That idea pretty much was the reigning metaphor for the ancients and alchemists of the middle ages. Fire in Greek is φλόξ, phlogo, and fiery is phlogistos.
First stated in 1667 by Johann Joachim Becher, he created the word phlogiston, and made phlogiston "separate" from stuff -"matter." George Ernst Stahl promoted and developed the theory of phlogiston. The word became dominant until 1783 when Antoine Lavoisier demonstrated that the associated concepts and writings of "The Theory of Phlogiston" was inconsistent.
In 1687, Newton was the first to define the word mass as a quantity. "The quantity of matter is that which arises conjointly from its density and magnitude. A body twice as dense in double the space is quadruple in quantity. This quantity I designate by the name of body or of mass." The word force was generalized in this context. Newton also used the term corpuscle, and his theory of light was dominant until Thomas Young had an alternative metaphor of waves.
Notions of atoms had been around since the Greeks, but the kinds or forms of mass, was developed later.
In 1600, the English scientist William Gilbert coined the New Latin word electricus from ηλεκτρον (elektron), the Greek word for "amber", which soon gave rise to the English words "electric" and "electricity." C. F. du Fay, who proposed in 1733 that electricity comes in two varieties that cancel each other, and expressed this in terms of a two-fluid theory. When glass was rubbed with silk, du Fay said that the glass was charged with vitreous electricity, and, when amber was rubbed with fur, the amber was said to be charged with resinous electricity.
One of the foremost experts on electricity in the 18th century was Benjamin Franklin, who argued in favour of a one-fluid theory of electricity. Franklin imagined electricity as being a type of invisible fluid present in all matter. For a reason that was not recorded, he identified the term "positive" with vitreous electricity and "negative" with resinous electricity. [Wikipedia, extracted, revised, emphasis added]
Roughly, during the same time period, Gottfried Leibniz, 1676–1689, coined the term vis viva (life force, Latin) to capture the notion of "the conservation of kinetic energy" in a vague way. In 1803, Young had put forth the wave theory of light, and Young, 1807, coined the word energy to subsume the specific concept of Leibniz, where upon that specific term vis viva fell in disuse.
The English word latent comes from Latin latēns, meaning lying hid. The term latent heat was introduced into calorimetry around 1750 by Joseph Black when studying system changes, such as of volume and pressure, when the thermodynamic system was held at constant temperature in a thermal bath. James Prescott Joule characterized latent energy as the energy of interaction in a given configuration of particles, i.e. a form of potential energy, and the sensible heat as an energy that was indicated by the thermometer, relating the latter to thermal energy.
Lavoisier argued that phlogiston theory was inconsistent with his experimental results, and proposed a 'subtle fluid' called caloric as the "substance of heat." Calor -- Latin for heat. According to this theory, the quantity of this substance is constant throughout the universe, and it flows from warmer to colder bodies. Indeed, Lavoisier was one of the first to use a calorimeter to measure the heat changes during chemical reaction. The word Caloric was used until the end of the 19th century. Lavoisier also had introduced the term element as a basic substance that could not be further broken down by the methods of chemistry. In 1805, John Dalton used the concept of atoms to explain why different elements always react in ratios of small whole numbers (the law of multiple proportions) and why certain gases dissolved better in water than others. He proposed that each element consists of atoms of a single, unique type, and that these atoms can join together to form chemical compounds. Dalton's theory was called "atomic theory."
The English chemist William Hyde Wollaston was in 1802 the first person to note the appearance of a number of dark features in the solar spectrum. In 1814, Fraunhofer independently rediscovered the lines and began a systematic study and careful measurement of the wavelength of these features. About 45 years later Gustav Kirchhoff and Bunsen noticed that several Fraunhofer lines coincide with characteristic emission lines identified in the spectra of heated elements. It was correctly deduced that dark lines in the solar spectrum are caused by absorption by atomic elements in the Solar atmosphere.
Gustav Kirchhoff created the phrase black-body radiation in 1862.
The term entropy was coined in 1865 by Rudolf Clausius based on the Greek εντροπία [entropía], a turning toward, from εν- [en-] (in) and τροπή [tropē] (turn, conversion). Building on Sadi Carnot's idea of the impossiblity of a perpetual machine, Clausius wrote the first quantitative description of something "disordered" related to heat is as a measure (quantity), in form of a real number. Josiah Gibbs fabricated an equation using the real variable S which referred to entropy, Ludwig Boltzmann in his papers developed a direct expression of it, from some general priniciples. Around the same time period the phrase "potential energy" was coined by William Rankine, whereas William Thomson (Lord Kelvin) coined the term "kinetic energy"
"In far from equilibrium conditions,
the concept of probability that underlies Boltzmann's order principle is no longer valid
if the structures we observe do not correspond to a maximum of complexions"
-- Ilya Prigogine
In 1887 the Michaelson-Morley light experiment could not detect the presupposed Greek "aether" and then most had assume to presuppose that a kind of "vacuum of space" existed. And the physicist J. J. Thomson, through his work on cathode rays in 1897, discovered the electron, and concluded that they were a component of every atom. Thus he overturned the belief that atoms are the indivisible, ultimate "particles of matter." Lastly, Marie Curie uncovered the mystery of "radioactivity".
At the turn of 19th century into the 20th century, it seemed to many scientists that nothing much was left to be done at a fundamental level. In the area of mathematics, some (like Piano, Cantor, Hilbert) were hoping either completely formalize or/and axiomatize the field. However, in the first decade of the 20th century, Albert Einstein and Max Planck discovered cracks in Newtonian Physics (called dynamics). And Bertrand Russell kicked the legs out from under Cantor's pedestal. Then finally in 1930, Kurt Godel demolished Hilbert's dream to completely formalize Mathematics.
"It is evident, that all the sciences have a relation, greater or less, to human nature: and that however wide any of them may seem to run from it, they still return back by one passage or another. Even Mathematics, Natural Philosophy, and Natural Religion, are in some measure dependent on the science of MAN..." -David Hume. A Treatise of Human Nature (Kindle Locations 148-150).
Maxwell in the 19th Century had unified electricity, magnestism, light forces by Maxwell's equations (later condensed by Heaviside) and his "ubiquitous (using the aether) mechanical gear and wave" metaphor. Newton's Forces, which included inertial and gravity, now included "electromagnetism." Besides inertial force, gravitational force, EM became another force also. There appeared to be a Hidden Order within physical objects.
Maxwell's diagram on the nature of electro-magnetism
So around the turn of the 19th century into the 20th, although there seemed to be few kinds of "particles" of matter given that there were these "things" called elements and the particle electron, there was no consensus what these particles were made of other than the vague folk term "matter," with the different associated number of different masses and possible charge. Some experts in the fields, such as Ostwald in chemistry and Mach in physics continued to hold out in accepting "atomic theory."
However, in the same 19th century some very microscopic fizzures and gaping holes appeared in the mathematics. With Abel, Bolyai, and Poincare's precise musings, the certainity of discrete or continuous mathematics started to separate and disappear, like Charles Dodgson's cheshire cat. Hidden Chaos was started to appear in mathematics and obviously that had a lot to do with the hidden chaos of physical objects.
Moreover, the question then became what kinds of chaos and what kinds of order are within an object.
With the advent of thermodynamics, the concept of black body radiation developed. What wasn't explicit about this development was a black-body was a theoretical construct, that is, in physics a black-body is really, typically, an ideal black body. The question was what was the "peak" of energy for an "object" in terms wavelength, and what was the shape of that curve based on temperature.
In 1900, Max Planck a theory based a formula that very well approximated the emission of energy in the ideal black body, but it had one glaring error, so he added an extra term which worked and by analyzing his ad-hoc formula he decided to use the word "quanta" (Latin quantas for how great) to represent an indivisible "packet" of energy, and assigned a constant number to that minimum of "wholeness" - which would later named Planck's constant h. 1905, Einstein further reenforced the word talking about what he called such a wave-packet the light quantum (German: das Lichtquant).
Who ordered that?
-- I. I. Rabi
In 1911, Ernst Rutherford published a model of the atom that had "big positively centrally located charged region" very small in size compared to the atom based on his experiments running up to that time -- with that he destroyed J. J. Thomson's pudding model. Later the word "atomic nucleus" was coined for that region.
Also in 1905, Einstein's special relativity started physicists thinking about these "particles" in motion for he linked a quantity of Young's energy E with Newton's quantity of mass M with the quantity of "speed of light" in a vacuum. However, Einstein's special relativity implicitly assumes equilibrium. The universe is not in equilibrium.
Finally in 1913, Niels Bohr was somewhat successful in a theoretical modeling the hydrogen atom's spectrum which invoked the physics community to try to model more complicated atoms (more than one electron) with varying success for the next 40 years by trying to model the atom by mathematical entities and math-matching their computations to Fraunhofer spectrum lines. Those models became more and more numerically accurate, with more quantum numbers. And more and more semantically complicated concepts (in the form of a corpus and lexicon of words), such as "quantized-angular-momentum."
Even though these particles of "matter" had different numerical numbers associated with them (e.g., atomic weights), there seemed to be definite patterns: discrete and continuous. The proton and neutron were discovered and name later in the first half of the 20th century. The problem was more "particles" kept "popping up," such that Rabi was prompted to utter his famous line.
Some were predicted. Like Dirac and Pauli had predicted the positron and the neutrino, respectively. However, there were phenonema (like the Lamb shift) and particles that "nobody ordered" (predicted or could explain).
Much of the advancement in prediction had come from applying special relativity to the particles, which in beginning was very hard to do.
In 1912 Albert Einstein realized that he could generalized his special relativity to "general relativity." Current physics has not been able to agree on any unitary model that merges "particle" physics with general relativity. We have the Standard Model built up by accretion and we have General Relativity. Of course, beyond that we have life.
Ersatz: The Problem with Modeling
In far from equilibrium conditions, the concept of probability that underlies Boltzmann's order principle is no longer valid if the structures we observe do not correspond to a maximum of complexions" -- Ilya Prigogine
"Cela leur a pris seulement un instant pour lui couper la tête, mais la France pourrait ne pas en produire une autre pareille en un siècle." -- Lagrange on Lavoisier
"I will never understand" -- Lise Meitner on Boltzmann's suicide
In 1776, there were four important documents published: 1) The Decline and Fall of the Roman Empire, by Edward Gibbon, 2) Common Sense, by Thomas Paine, 3) The Declaration of Independence, by Thomas Jefferson, and 4) On The Wealth of Nations, by Adam Smith. It took another century for those ideas to work their way in a more precise way via another major development in science in the 19th century as the notion of "evolution" -- Lamarack, Lydell, Smith, Wallace, and culminating in Darwin with the publication of On the Origin of Species in 1858.
Ludwig Boltzmann was inspired Darwin's work, and he tried to apply these circle of ideas to thermodynamics. He made a brilliant mistake. He analyzed his gedanken world as an isolated system. His analysis works very well for "conventional" physical analysis: it has worked for "simple systems" -- simple analysis. His model worked very well for about a century. However, the analysis "doesn't" do very well for systems long-term (billions of years) or more complicated systems (like life and quantum systems). His model included a limited concept of "temperature."
The Pythagorean … having been brought up in the study of mathematics,
thought that things are numbers
… and that the whole cosmos is a scale and a number.
–Aristotle
The problem of the notion of physical "temperature" is that it is just a scale and number. A thin concept. And it is not uniformly distributed through space and time, energy and mass. It is an average (by the way of a sampling) assuming that the environment is at an equilibrium. In reality, there are different temperatures at different places and times (energy and mass) depending on how you measure it. It begs the question: what determines the distribution of heat ex-ternally and in-ternally?
Of course, the simple and complex answer is "information".
The problem of with that "simple" and "complex" answer is "in-form-ation."
The word inherently is not explicitly refering to half the issue: what about the "ex"-form-ation" or in simpler venacular what is the context of "the information" of the "system." Contexts (or environments) change: the universe is always changing.
Death starts when internal change happens slower than external change
- David M. Keirsey
The limits of "information"?
“Fix reason firmly in her seat,
and call to her tribunal every fact, every opinion.”
— Thomas Jefferson
When logic and proportion have fallen sloppy dead
And the white knight is talking backwards
And the red queen's off with her head
Remember what the dormouse said
Feed your head,
Feed your head
--Jefferson Airplane
The some of the ancient Greeks rejected the prevailing morality, religion[myth] as basis for understanding their world, and started "science". Some historians credit, Thales as the father of science and the first to use deduction in Thales Theorem. Whether or not he or Pythagoras did it, it does not matter. Parmenides and Zeno also entered the discourse in discussing "truth" and "opinion", introducing the paradoxes between discrete/continuous and self reference. Science and reason progressed haltingly, with Aristotle positing and discussing "logic". Logos - Greek for word, speech. Aristotle used the word logos to mean "to reason." In 300BC, Euclid wrote about a method of finding primes. Euclid also compiled geo-metric "postulates" and "theorems" in Euclid's "Elements".
Archimedes used mathematics and his reasoning to design and implement many of his work or war machines. Archimedes looked at the "tiling problem" and form of a rudimentary combinatorics. He wrote a letter to the librarian of Alexandria titled The Method of Mechanical Theorems
Not much development strictly in "logic" was done after the Greeks until the Enlightenment and the industrial revolution, humanity could only speculate in form of natural language using the vague Natural Philosophy or "natural reasoning", few contributed, in shedding clarity to "logic" and "computation" as for example, William of Ockham [Ockham's razor]. In a more mathematical vane, Pascal's triangle (combinatorics) was known by several people throughout the ages and the Muslim Abu Jafar Muhammad ibn Musa al-Khwarizmir introduced of the place holder 0 [zero] from India into the Arabic numbers with a decimal system and helped develop Algebra. With Stevins the natural counting numbers and fractions became easier to write down. Using that notation, Charles Napier developed "logarithms."
Rene Descartes proposed techniques and a perspective [Analytical Geometry and Materialism] and Gottfried Leibniz pre-staged the notion of binary forms[Monads]. The adjective real in this context was introduced in the 17th century by Descartes, who distinguished between real and imaginary roots of polynomials. Implicit computation by human effort in the form of "numbers" and "geometry" was developed extensively. Newton and Leibniz devised "calculus", with the notion of the "infinitesimal" echoing Zeno.
Read Euler: He is the master of us all.
In the early part of the 1800's Carl Gauss, Nikolai Lobachevsky and Janos Bolyai broached the subject of non-Euclidean geometry. Gauss also thought up the complex numbers. Gauss declared Number Theory as the Queen of Mathematics.
Roughly in the same time period, in 1801, Jacquard's loom was demonstrated with "punched cards," that mechanically controlled the weaving patterns of the loom. In 1822, Charles Babbage started work on a Difference Engine which was designed solve polynomial equations. The failure to make the Engine prompted Babbage to design the Analytical Engine. The Analytical Engine which incorporated the idea of using punch cards. In 1841, Ada Lovelace understanding Babbage's design speculated about what ultimately what could be done with such devices, pre-staging the notion of computation. She also designed a procedure for computing Bernoulli numbers via the Analytical Engine, such that she could be said to be the "first programmer".
In 1822 Joseph Fourier explored in his book the notion of dimension. On the other hand, in 1823, Niels Henrik Abel in trying to solve quintic equations, discovered a proof that there are no general algebraic form solutions for all polynomials of five degree or greater. And in 1832 there was young man left a legacy who developed a way of characterizing solutions to equations in discrete ways, his name was Evariste Galois. His notion of permutations along with Pascal's notion of combinations were developed by Joseph-Louis Lagrange various ways of solving and not solving equations exactly. Group theory developed from there.
At a similar time frame William Hamilton in 1843, devised Quaternions, several people seeing Hamilton's quaternions, devised Octonions.
"What are numbers and what should they be?"
Was sind und was sollen die Zahlen?
-- Richard Dedekind
George Boole in 1854 published An Investigation of the Laws of Thought (1854), on Which are Founded the Mathematical Theories of Logic and Probabilities
Arthur Cayley[tables], Sylvester [invariants], Dedekind[cut], Cantor[ordinal, cardinal], Poincare[chaos,order], Peirce[logic]
On January 8, 1889, Hollerith was issued U.S. Patent 395,782
Hollerith[physical computation], Morse[digital communication], Bell[messages], Noether[ideals], Turing[series versus recursion], Moufang[diassociative rings], Von Neumann [quantum entropy]
Norbert Wiener, Cybernetics: Control and Communication in the Animal and the Machine, 1947.
Rereviewing the book I picked up in 1967, that I mostly didn't understand at the time, I can see why now (besides being an ignorant 17 year old). A following sentence has been on my mind for almost 50 years. The question is what did it mean?
"It is simpler to repel the question posed by the Maxwell demon than to answer it. Nothing is easier than to deny the possibility of such beings or structures. We shall actually find that Maxwell demons in the strictest sense cannot exist in a system in equilibrium, but if we accept this from the beginning, and so not try to demonstrate it, we shall miss an admirable opportunity to learn something about entropy and about possible physical, chemical, and biological systems. For a Maxwell demon to act, it must receive information from approaching particles concerning their velocity and point of impact on the wall. Whether these impulses involve a transfer of energy or not, they must involve a coupling of the demon and the gas. Now, the law of the increase of entropy applies to a completely isolated system but does not apply to a non-isolated part of such a system. Accordingly, the only entropy which concerns us is that of the system gas-demon, and not that of the gas alone. The gas entropy is merely one term in the total entropy of the larger system. Can we find terms involving the demon as well which contribute to this total entropy? Most certainly we can. *****The demon can only act on information received, and this information, as we shall see in the next chapter, represents a negative entropy.*****
"At about the beginning of the present [20th] century, two scientists, one in the United States and one in France, were working along lines which would have seemed to each of them entirely unrelated, if either had had the remotest idea of the existence of the other. In New Haven, Willard Gibbs was developing his new point of view in ****statistical mechanics****. In Paris, Henri Lebesgue was rivalling the fame of his master Emile Borel by the discovery of a revised and more powerful theory of integration for use in the study of ***trigonometric metric series****. The two discoverers were alike in this, that each was a man of the study rather than of the laboratory, but from this point on, their whole attitudes to science were diametrically opposite. Gibbs, mathematician though he was, always regarded mathematics as ancillary to physics. Lebesgue was an analyst of the purest type, an able exponent of the extremely exacting modern standards of mathematical rigor, and a writer whose works, as far as I know, do not contain one single example of a problem or a method originating directly from physics. Nevertheless, the work of these two men forms a single whole in which the questions asked by Gibbs find their answers, not in his own work but in the work of Lebesgue."
Norbert Wiener. Cybernetics, Second Edition: or the Control and Communication in the Animal and the Machine (Kindle Locations 950-951). Kindle Edition.
But the physicists (like Gibbs) and mathematicians (like Lebesque) cannot look to statistics (statistical and quantum mechanics) and the continuum via trigonometric series, to solve a problem they created. Gibbs, Lebesque, and Wiener could not solve the problem they help to create by not understanding "information" at an enough sophisticated level. They restricted themselves to only using "time" and "space" as to holding that "information" -- and mass and energy are in "balance" -- or "equilibrium".
Shannon [information entropy], Golay[finite enthalpy, Cristofell symbols], Hamming[codes].
Claude Shannon, an electrical engineer, published in 1948 "A Mathematical Theory of Communication"
They (Shannon attributed it to John Tukey) "coined" the neologism -- bit (binary digit). Shannon, having read Boole's treatise, started building electronic digital circuits, for before the telephone network was strictly analog.
Information as a measures: entropy.
The mathematical theory of information is based on probability theory and statistics, and measures information with several quantities of information. The choice of logarithmic base in the following formulae determines the unit of information entropy that is used. The most common unit of information is the bit, based on the binary logarithm. Other units include the nat, based on the natural logarithm, and the hartley, based on the base 10 or common logarithm.
Mealy[, Moore[semi-groups, Wisconsin], Kleene[inference, computation, proof], Mandelbrot [edge of chaos, edge of order],
Exformation as a metric: enthalpy.
'Problems cannot be solved with the same mind set that created them.'
-- Albert Einstein.
There is the issue of the continuum versus quanta, that has not be resolved to this day by the physics and mathematical communities. It should be noted that: The universe (as a whole) is not and never has been in equilibrium.
On the other hand, Wiener in identifying "information" as important factor, points the direction, but not the path out of the problem. And it took Robert Rosen, a mathematical biologist, to point to a pathway out of the problem.
Marie[replication/dissipation], Mendeleev[patterns]
Ackley[hierarchy of abstraction],
What does "information" mean?
Jacob Bekenstein [conformal, meromorphic]
In physics, the Bekenstein bound is an upper limit on the entropy S, or information I, that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximum amount of information required to perfectly describe a given physical system down to the quantum level. It implies that the information of a physical system, or the information necessary to perfectly describe that system, must be finite if the region of space and the energy is finite.

Eric Verlinde
Entropic gravity is a theory in modern physics that describes gravity as an entropic force; not a fundamental interaction mediated by a quantum field theory and a gauge particle (like photons for the electromagnetic force, and gluons for the strong nuclear force), but a probabilistic consequence of physical systems' tendency to increase their entropy. The proposal has been intensely contested in the physics community but it has also sparked a new line of research into thermodynamic properties of gravity.
How does "heat/mass/energy" change -- evolve?
It depends on internal and external factors. What is internal? What is external?
With the particle model an element of "mass" is considered constant. The momentum is separated to be multiplicative factor. What justifies that? p=mv=m(ds/dt) (but as we all know v is a momentary fiction). What Boltzmann assumed in his analysis, was linear momentum was the only factor. Angular momentum (in some sense "constant"-linear) was also added.
Internal symmetry and external symmetry.
static equilibrium, dynamic equilibrium, non-equilibrium -- poles and zeros: sources and sinks.
Internal Energy (kinetic, potential) Heat (Latent Specific,
Black [latent], Thomson
Potential energy, Kinetic energy. (Hamiltonian, Lagrangian)
Mass
The word space has used by English speakers for many centuries, it was elaborated and vastly complicated by mathematicians and physicists, from the 1800's to including the mind bending, for example, a Calabi-Yau Space, based on the changing model from a basic 3D Euclidean space, which was implicitly assumed by laymen to this day, to more complicated possiblities. Berhard Riemann and Felix Klein taking their cue from among others, Bertrami and Sophus Lie literally opened up the notion of space.
What is "space"
Time! Time.
Bilbo Baggins
I do not have the time.
Evariste Galois
What is time?
Time is either everything or nothing at all.
?Julian Barbour?
There is a problem. In physics, the conventional use of word time, and as a variable in equations, it is usually regarded as a "single dimension" model by R1. Why?
Einsteinian time, assumes a universalism very much like Newtonian space. Although typically "entangled" as in "spacetime" for example, in a 3+1 Minkowski space, "time" is an unrestricted continuous (modeled as a "real number") value. It is true, Hawking has played around with "virtual time" in using a "two dimensional" notion of time, as represented in a complex number. And lastly, Petr Horava has broached the subject by a hint of freeing time from the historical strait-jacket of conventional physics. But these efforts are hampered by their myoptic concentration on the limited processes in physics (and the physics community limited understanding of "open systems"). Scientific fiction, that is, speculation on the nature of multiverse has not really added to new and precise use of time, but it is popular on TV. Life, as a metaphor for physics been broached, but the notion of time as still conceived as as single dimension entangled in "spacetime."
The recent proving of the Poincare Theorem, used a notion of a reduced length that had a interesting use of "time" in part of a metric, in a form of a functional.
Is it crazy enough?
Niels Bohr
What is time?
Robert Rosen has a whole chapter on different uses of the concept of time [Anticipatory System, Chapter 4, Encodings of Time]. So I would submit, time needs to be examined in context. Einstein did a detailed gedanken experiment with "light" and "time" but he did not examine closely the concept of "an event." What is "an event" -- this concept needs to be looked from an "information theoretic" and and "exformation theoretic" perspective. Current theories fail to account for life (the complex) and quantum mechanics (the small) suggests there needs to be another set of gedanken experiments.
In physics: mass, energy, space, and time are treated as measures, which are related, but "space" and "time" are concepts whereas "mass" and "energy" are percepts. In other words, space and time do not physically exist (nor does spacetime, e.g., 3 + 1, exist either as a simple construct), whereas mass and energy do physically exist. Now, having only one dimension of time, is mathematically and conceptually simple, but it maybe no longer be productive to have that simple of an encoding. It is time to consider "multiple dimensions of time," or "kinds of time". But before that one must examine the nature of reality, reference, inference, and reasoning.
Counting can be very different from measure -- and Time as commonly used is ambiguous, and often very different from "measure and time."
There are "kinds" of "time" in scientific jargon -- Counting "time" (N in mathematics) (entropy/synergy in "physics"), Discrete Ratio "time" (Q and Z in mathematics) or ("duration" in physics), Indeterminate Ratio "time" (for example, computable numbers in mathematics) or (measurable time/space(?spacetime?) in "physics"), and process "time" (Octonions, for example in Mathematics) (age in "biology")
Physics' "time" is normally abused and associated with R, the "real" numbers.
Robert Rosen in Anticipatory Systems wrote about "The Encodings of Time:" 1) Time in Newtonian Dynamics, 2) Time in Thermodynamics and Statistical Analysis, 3) Probablistic Time, 4) Time in General Dynamical Systems, 5) Time and Sequence: Logical Aspects of Time, 5) Similarity and Time, 6) Time and Age.
Let's look at something that physics has said -- energy and mass are related. Of course, Einstein has found a "law" that seems to apply to most of the current Universe. But we know that if there was a "big bang" that his "law," E=mc2, does not apply "at the beginning" -- So what gives? Let us do a simple gedanken experiment on the Universe.
Consider the equation E/c=mc. This is just a rewrite of Einstein's equation.
First let's unpack this equation. c is the speed of light, assumed to be a constant by Einstein. Since it, c, is a constant, let us assume a different amount of information that involves that "constant." For example, consider a "precise" constant like e, Euler's number. Euler's number has, given enough time, -- an infinite amount of time -- it contains (or generates) an infinite amount of information. So what if we decide to represent c as a constant with an infinite amount of information. Now c as a constant has units associated with it: c = D/T, that is distance over time. So let us rewrite the equation again. E/(D/T)=m*(D/T)
So if those who like real numbers (that can represent an infinite amount of information) might stick in a real number constant. Let us chose our units so for energy E = 1, and mass m = 1. (That is we will count the Energy of the Universe = 1, and the Mass of Universe = 1, and the time of the universe as 1. So let's rewrite the equation, using these unit choices. 1/(D/1)=1*(D/1).
Simplifying. 1/D=D. Of course this "doesn't seem to make sense." (unless you use D=1) -- Maybe this demonstrates the Universe does exist. However, what does it mean from an informational point of view. If I use a "infinite information constant," is there any 'choice" that does make some sense? How about the "constant" ∞. So 1/∞ = ∞/1. You jest -- most people would say. But could you physically tell the difference between 1/∞ and ∞/1? Both require explicitly an infinite amount of information -- like 0 does implicitly. (Yeah, you have to think about that for awhile -- there are no short cuts in this idea).
Time is everything and nothing at all.
David Keirsey
Fabrication of the dialectic. Fabrication of the quadalectic. Fabrication of the octalectic ...
Fichtean Dialectics (Hegelian Dialectics) is based upon four concepts:
The question is how does one use this kind of encoding to any use. Obviously religion and philosophy do not have much to add, if anything to contribute here. Science and mathematics has something to contribute, but one has to be very careful because the fabrication of Science and Mathematics is ad-hoc and not systematic. And Hegel and Fichte ideas are hopelessly vague, and their notion of time is like all others: too simple.
How can one, change and make these vague concepts more precise and useful?
Formatics: Relational Science and Comparative Complexity
Structure and Function.
So you if you look from an informational point of view, 1/∞ ≡ ∞/1. Thus the INTERNAL UNIVERSE (?multiverse?) ≡ EXTERNAL UNIVERSE (?our universe?). Hyper-Space (?quantum world?) is homeomorphic to the Euclidean-Space.
Hidden Chaos. Hidden Foundational Dynamic Chaos. Hidden Ethereal Dynamic Chaos
Hidden Order. Hidden Foundational Dynamic Order. Hidden Ethereal Dynamic Order
The second part of the first phenomenological issue is what kind of context is the massive dissipative/replicative structure in. Clearly, if the dissipative/replicative structure is growing or shrinking, then the structure is either growing or shrinking because of itself, or the surrounding context is adding or subtracting to the process-structure. It is important to connect, at some level of abstraction, a particular structure within the total context, that is, the universe, both in material and functional terms. The overall analysis of material complexity is the first, and easiest thing to do. The following is a defining the basic structure of material complexity so to give an overarching context.
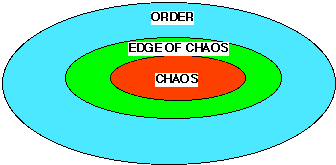
Three basic regimes within a dissipative/replicative structure in terms of material complexity have been defined: chaos, order, and the edge-of-chaos/edge-of-order.
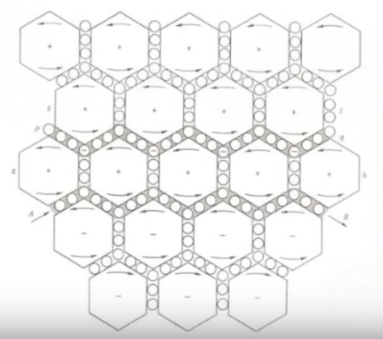
A Dissipative/Replicative Structure: A Macrosystem
The edge-of-chaos metaphor (and it associated mathematical and computational methods: Crutchfield, Mitchell, and Langton) is useful in describing massive dissipative/replicative structures. Every massive dissipative/replicative structure is on some edge-of-chaos, and some structures are part of multiple levels of edge-of-chaos. A large part of the edge-of-chaos metaphor involves both a macro-process and a macro-structure. But also it includes micro-structures and micro-processes. The combination of macro-process, macro-structure, micro-processes, and micro-structures will be the basis for the metaphor.

The edge-of-order metaphor is a new metaphor borrowed from the edge-of-chaos metaphor, to make crucial link to the other important metaphor of replication and link it to the notion of life, which also applies to non-life phenomena. It is important to realize the edge-of-order is the same as the edge-of-chaos, but viewed from a different point of view. For Darwin's metaphor of evolution can be applied to non-life systems, because some kind of replication exists in these systems.
![[Edge of Chaos Edge of Order]](images/eofceofo.gif)
The material complexity of the universe can viewed as a processes of successive layers of chaos, order, and the edge of chaos/order, there by called involution.
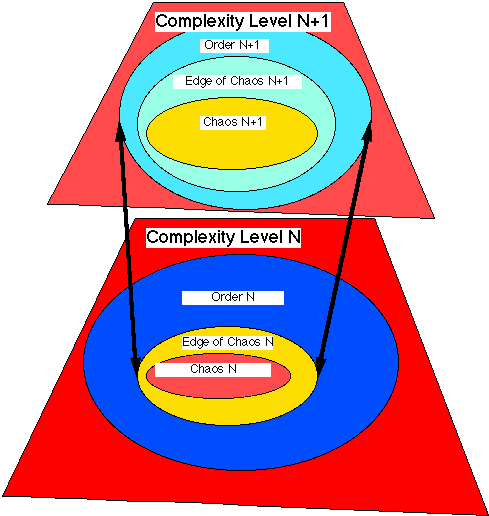
Two Levels of Major Material Complexity
In this regard, I define two important classes of dissipative/replicative structures: microsystems and macrosystems. These two classes are dissipative/replicative structures at the major levels of material complexity. They clearly exhibit a property of "self-organization," although what "self-organization" means is problematic. For now I will use the vague (and oxymoronic) notion used in the science of complexity community.
Macrosystems are evolved from being a massive part of the universe and are massive dissipative/replicative structures, such as galaxies, star systems, planets, Gaia, and Hypersea; they being the primary instantiation of "context" from which other massive dissipative/replicative structures are embedded.
Microsystems are the building blocks of our existence, the ordered structured processes that embed invariant information in our world, such as, quanta, particles, atoms, molecules, cells, organisms, families, societies, and cybersocieties. Microsystems are contained within at least one macrosystem, and typically are embedded in several macrosystems and microsystems, which in the configuration of those macrosystems and microsystems constitute their context. Microsystems are also dissipative/replicative structures, although physicists would argue whether quanta are dissipative or replicative. But the physicist has no satisfying ontological explanation of quanta. Again, since the physicist use the English description of "spontaneously emit" or use statistical mathematics to describe quanta, one can use the words "dissipative" or "replicative" depending on the context versus "spontaneously emit or decay" because they very close in their macro behaviors (if you don't know what they consist of).
The third form of dissipative/replicative structure are the subsystems . Those are entities that are not easily defined from simple discrete and finite compositional forms of macrosystems and microsystems, being that they are primarily part of a major material macrosystem or microsystem and their involutionary(evolution of complexity and evolution) status is ambiguous. Their ultimate fate is largely determined by their current position in their surrounding dissipative/replicative context rather than their inherent self-organization.
The current use of the word "system" is typically a subsystem. As for example most people would classify a refrigerator is a "system." However, one does not usually include wires to the power plant, the power plant, and the human society that runs and maintains the power plant, which has a great deal of influence on the "behavior," "causality" and "functionality" of this refrigerator in its actual operation. Some properties of the refrigerator, its color, weight, its storage capacity, its predicted efficiency, etc., are clearly not dependent on this ignored context, but the context does play a part in some situations. Depending on a scientist's goal, what part of the context is ignored or assumed when studying or characterized often goes unexamined.
A big problem in science has been the general use of the word "system" to talk about all of these three types: macrosystems, microsystems, subsystems, and any arbitrary groupings (sometimes more properly called ensembles). When discussing and characterizing these "systems" many of the underlying assumptions about the general properties of these "systems" are not explicitly detailed, often adding to the confusion. A common situation for most science, is the underlying assumptions are long forgotten or never taught so to make progress in application of well proven techniques. The separation of life sciences versus the physical sciences has been largely dictated by different techniques, and those techniques are couched in overlapping words and scientific assumptions.
By analysis and synthesis one can characterize our involution of the universe in terms of major levels of material complexity as follows.
However, the advantages of words, with their inherent semantics being ambiguous, abstract, concrete, and definite cannot be avoided. They are the only things that can refer to things and processes in the real world. Words are the most meaningful things that can serve as encodings and decodings of reality.
Com plex com- with, plex plexus (ply or to fold)
All is flux Heraclitus
If one tried to use the wave model for explaining the universe, one would come up with two major problems. First, the universe does not appear continuous. In fact, continuity is an illusion, because it assumes infinity in the small. Second, the wave model assumes an underlying material existence, which must be at some scale. Mathematically, using the continuous wave model and its associated mathematics, one quickly gets into degenerancies of matching or harmonic frequencies. On the other hand, Ilya Prigogine has analyzed Poincare resonances (degenerancies of waves) and shown how higher level "particles" ("static" dynamic waves) could appear spontaneously based on continuously (in time) ordered interaction of smaller particles (constituting the wave medium). Prigogine also showed how higher level particles would disappear spontaneously when the interaction of smaller particles is continuously (in time) random.
All is atoms and void Democritus
If one tries to finesse the issues of continuity by postulating or measuring structures, in other words: the discrete, the problems don't go away. Hypothesizing the "discrete" always entails the question of 'what constitutes the discrete'? Discreteness assumes infinity in the large. The notion of structure and its extreme form a "point", called "particles" or "quanta" with the real world, must assume either an external definite ordered "state" (for example, position and velocity) or a "probabilistic" or in the extreme an internal indefinite random "state."
Robert Rosen has shown either assumption (continuity or discreteness) leads to a limiting form of entailment. But you can choose when and how to do the intertwining of those assumptions when comparing and contrasting analogous models, or generalizing out the self-referencing, and therefore contradictory (or rather, circular) details.
The formation of structures at radically different scales is not well treated by any known mathematics, certainly not by dynamics or statistical mechanics, for they only treat one or two levels of complexity. Fractals and chaos theory has some notions of scales, but still hasn't addressed a multiple level of complexity aspects in a significant way: that is there is no significant interaction between objects at different scales. Renormalization is the closest to dealing with the issue but is an approximation (it has a finite cutoff value).
Fractals are infinite objects, but when the fractal converges (or diverges to the "small" infinity), one can represent that infinite object with an ideal object centered some "constant" value (typically represented as a "real" number). However, other fractals do not converge, but diverge to various kinds of large "infinity". This dichotomy is related to the two-body and three body problem.
The three body problem does not have a closed form solution (the energy is not integrable: its not finite). Poincare showed this mathematically. In the process, he opened up the door to understanding why the world is complex. Prigogine has elaborated further to relate classical notions of dynamics (read this as "understandable" notions) to why quantum mechanical notions (read this as "measurable" notions) have been successful in measurement but not understandability.
All dissipative/replicative structures must be characterized at all levels of complexity that they contain. At the lowest level of complexity, a material discrete-finite continuity must be assumed, but is also self-contradictory. For all three concepts (discrete, finite, continuity) implicate (continuity, infinite, discrete) their opposite, ala Zeno's paradox. The material basis must be assumed at some scale: discrete and finite, but it is possible one can use the functional basis to ground the local material (small dimensions) to the global functional (large dimensions).
Dissipative/Replicative Structures
Examples:
Macrosystems: Our Universe, Milky Way Galaxy, Sol: Solar
system, Jupiter, Earth, Gaia, Hypersea, Metaman.
Microsystems: a gluon quanta, an electron quanta, a proton particle,
an omega particle, a helium atom, a carbon-12 atom, a water(H2O) molecule,
a prion molecule, a Halococcus cell, a Hyella cell, a Tridacna
organism, a butterfly organism, an ant colony (family), a human family,
a Mayoruna tribe (society), The US government (society), Microsoft corporation
(society), The World Wide Web (cybersociety).
Subsystems: photon, gamma rays, superconducting electron pair,
Einstein-Bose condensate, ion, cation, Ryberg atom, a viriod, a virus,
a gamete, a skin cell, an ant, an orphan, a website, in bankruptcy dot.com
company, a viral email joke.
Caveats:
The Universe is defined by mass, energy, space, and time. Of course, we don't understand what "mass," "energy," "space" and "time" are in terms of other notions. Except the physicists can tell us how to "measure" them. That is physicist's concepts of mass, energy, space, and time are phenomenologically: measures. Physicists know a great about the most likely relationship between them ( in a statistical manner - i.e., we don't know the underlying ontological relationship).
The inherent information embedded in the population can mostly determine the "involution" or "self organization" assuming a relatively (depending on the complexity of population) stable flow energy (communication) into and through the dissipative/replicative structure. There is no such thing as a dissipative/replicative structure that is not embedded and part of a surrounding dissipative/replicative structure. The classic example of pervasiveness of a surrounding dissipative/replicative structure is the expanding the space with the remaining background radiation of the universe.
Besides boundaries of "in/out" there is the boundary of the "large" and "small". The universe's boundary is probably having to do with a self-referencing at the large and small boundary. It is noted that the boundary between the Meta-Universe and the Universe is problematic both in conception and definition. It probably has to do with the confounding of "in/out" with the "large" and "small". For boundary at that level of complexity of the universe, large/small and in/out are probably the same.
"Organization" is the other part of characterization of communication. The spatial and process distribution within levels of complexity determine the "self-organization" . Macrosystems and microsystems both have self-organization that can be characterized, in a rough-cut manner, by composition of three regimes of matter: chaos, order, and the edge-of-chaos/edge-of-order. The kinds of chaos, order, and the edge-of-chaos/edge-of-order does matter at each level of complexity.
The relationship between "replication" and "dissipation" is crucial here. Dissipation is a form of replication, and replication is a form of dissipation. Dissipation can be viewed as "replicating" randomness (chaos). Replication can be viewed as "dissipating" order. The crucial insight is to realize there are different kinds of chaos and different kinds of order, so there are many forms of dissipation and replication depending what kind of order and chaos are being dissipated or replicated.
It might be assumed that Energy(in the form of light-bosons - photons) maybe the communication between the universe and the meta-universe.
For example, let the context C be the solar system, and the dissipative/structure structure D be the planetary system of Earth (including the moon). The Earth is on the edge-of-chaos relative to the solar system. Currently, the mass and temperature of the sun is conducive to the future "self-organization" of the Earth. Mercury is too close to the sun to be on the edge-of-chaos, so it does not have much of an atmosphere (gas phase) or any liquid phase, and Uranus is too far and is too frozen to be on the edge-of-order of the solar system.
The "populations" within and without a dissipative/replicative structure depends on looking at the level of complexity. In massive dissipative/replicative structures, generally the "chaotic regime" population is 10e7 larger in population to the "edge-of-chaos" population in terms of "mass and energy." What "mass and energy" *is* depends on the complexity. In addition, the "order regime" population is 10e7 larger in population to the "edge-of-chaos" population in terms of "space and time." What "space and time" *is* depends on the complexity.
The general properties of a dissipative/replicative structure depend on the envolution and involution of the structure. In addition, the surrounding context has a great role, depending on what state of context and the relationship with the dissipative/replicative structure in the Chaos/Order scale. Some of these general properties can only be characterized by asking why questions, including the surrounding context. On the other hand, most scientists are only interested in properties or characterization of structures and processes, ignoring the surrounding context. The context is assumed to be in "equilibrium." For example, most biologist are only interested "life" and how it operates. Physicists are interested in "non-life," and how it operates. Few biologists are interested in what is life. That is, what are the general properties of life on earth? Or more specifically, what are the general properties of life, irrespective of our particular example on earth. Biologist see as "what or why life", either impossible or difficult to answer. Besides biology, few physicists are interested in why "non-life". Physicists consider why "non-life" questions (for example, why neutrinos?) not the province of science. However, Robert Rosen has shown the way to possibility of answering some of these why questions by a process of analysis and synthesis, and I further assert that the best way to do this is by examining contexts through comparison of models across disparate natural systems.
If the "temperature" of E is high relative to the major population of E, then most of the mass of E will be in the chaotic regime. If the "temperature" is low relative to the major population of E, then most of the mass of E will in the order regime.
Chaotic regimes are relatively homogenous in population type based on the highest level of material complexity. Chaotic regimes of N level of material complexity do not have any or relatively few entities of N+1. Order regimes are relatively homogenous in population type: order regimes have a majority of N+1 entities, but can have entities of complexity higher than N+1. Within a level of material complexity the chaotic regime has less material complexity in microsystems than the order regime.
The description of Dissipative/Replicative processes is in the context of a global Dissipative/Replicative structure (the so-called multiverse), but at the most primitive level, one cannot talk about what it is constituted of. One must posit almost complete randomness and almost complete order as the context, but the form must have the property of dissipation and replication.
Assumptions:
"Energy" finite (but not measurable), Space&Mass definite,
"Time" not finite.
Replication and Dissipation are complementary as well as entangled.
Distribution is a form of communication through dissipation and replication.
Distribution in energy is: matter (or constant information) in "energetic" motion (random information in process). Distribution in space is a fixed amount of matter (or information) in more space(patterned information in process). Distribution in time and structure is: correlation of "bits" of matter in time (patterned and random information in process).
In other words, communication is the changing of patterned information, whether it be random (nothing pattern) or ordered (something pattern). Dissipation is a form of distribution of communication, where the encoding or decoding of information is based on either communication in energy, time&structure, or space. Replication is a form of distribution of communication, where the encoding or decoding of information is based on either communication in energy, time&structure, or space.
The following is a table is a possible functional description of how
the problem solving metaphor might delineate the functional levels of complexity
in our involution.
| Complexity 0: Multiverse vs Universe: The Problem of Existence and Non-Existence (what to exist => material systems: macro dissipation, micro replication) |
| Complexity 1: Universe vs Galaxy Systems: The Problem of Dissipation and Replication (how to dissipate and how to replicate = time, energy versus space, matter) |
| Complexity 2: Galaxy Systems vs Star Systems: The Problem of Stability and Instability (what to make(replicate) stable and what not to make(dissipate) stable) |
| Complexity 3: Star Systems vs Planet Systems: The Problem of Control and Non-Control (what to control (replicate) and what not to control (dissipate)) |
| Complexity 4: Planet Systems vs Gaia: The Problem of Inheritance and Non-inheritance (what to inherit (replicate) and what not to inherit (dissipate)) |
| Complexity 5: Gaia vs Hypersea: The Problem of Mortality (what to live (replicate) and what to die (dissipate)) |
| Complexity 6: Hypersea vs Metaman: The Problem of Knowledge (what to know (replicate) and what not to know (dissipate)) |
| Complexity 7: Metaman vs Cybersocieties: The Problem of Learning (what to learn (replicate) and what not to learn (dissipate)) |
| Complexity 8: ? |
I suggest comparative complexity as methodology that can help in the analysis and construction of scientific theories. The first part of this methodology is using material complexity to delineate the major levels of complexity in massive dissipative/replicative structures. The second part, the use of functional complexity, has not been developed, but using the hints of Robert Rosen as in his {M,R} model (metabolism and repair), one can build numerous functional models. For example, one can develop the briefly outlined functional complexity levels in the neo-Hegelian model of replication and dissipation discussed above. The next step would be construct of a set of formalizations will involve using material complexity models and functional complexity models and relating those models via reference complexity models.